Conceptos básicos de Tracción Ferroviaria

Las ecuaciones de dinámica ferroviaria se basan en todo momento en evaluar la capacidad aceleradora del tren (esfuerzo de tracción provocado por los motores), las fuerzas resistentes a la tracción (resistencia a la rodadura, rozamientos internos de la locomotora, rozamiento con el aire circundante, rozamiento por inscripción del vehículo en curva) y sumarles o restarles el efecto de la fuerza de la gravedad debida a la pendiente del trazado.

La aplicación de todas estas fuerzas a la masa del tren generará un movimiento. Si la suma de todas estas fuerzas es positiva el tren podrá acelerar su marcha. Si la suma total es negativa el tren disminuirá su velocidad. Si el maquinista decide no usar la fuerza motriz del motor, el movimiento del tren dependerá de las fuerzas de rozamiento y de la fuerza de la gravedad; es el denominado “movimiento en deriva”. A continuación se analizan todos los elementos que intervienen en el fenómeno a estudiar:

- - - Esfuerzo de tracción (acelerador).
    - Fuerzas de rozamiento (deceleradoras).
    - Fuerza de la gravedad (aceleradora o deceleradora según estemos en pendiente positiva o negativa).
    - Fuerza por inscripción del vehículo en curva (si bien es una fuerza más de rozamiento y por tanto deceleradora, se suele considerar de forma independiente al resto de fuerzas de rozamiento).
    - Masas del tren (rotativas y no rotativas).

Esfuerzo de Tracción

Los motores de las composiciones ferroviarias transforman la energía eléctrica o la energía del combustible en energía mecánica. La capacidad de generación de tracción por parte de los motores depende de la potencia de los mismos. A partir de una potencia determinada, la fuerza que es capaz de generar el motor en cada instante no es constante, sino que depende de la velocidad que en ese momento lleve la composición. Partiendo de la ecuación de la potencia:

Potencia = Fuerza x Velocidad

En esta ecuación, al ser el término de la potencia un valor constante, la fuerza irá disminuyendo a medida que la velocidad aumente. Se genera así la llamada hipérbola teórica de tracción del motor, dado que la gráfica de la ecuación anterior es una hipérbola, siendo el eje de abscisas la Velocidad y el eje de ordenadas la Fuerza. Según dicha ecuación, a bajas velocidades la fuerza generada por el motor podría ser muy alta. De hecho, en una hipérbola teórica cuando la velocidad fuera cercana a cero, la fuerza se aproximaría a infinito, aspecto que resulta físicamente imposible.

En la práctica, la curva de potencia del motor no es exactamente una hipérbola, sino que es una curva que se asemeja en cierta medida a una hipérbola. Esta curva es suministrada por el fabricante de la locomotora y resulta fundamental en la modelización y análisis de la dinámica y cinemática ferroviarias. No resulta complejo localizar a través de internet curvas de potencia reales de distintas locomotoras y automotores, bien a través de los fabricantes, bien a través de los operadores ferroviarios que las alquilan.

Por otra parte, existe un factor limitante en la capacidad de generación de tracción de los motores: la adherencia rueda – carril. Si generamos un giro excesivo de las ruedas se puede superar el valor del rozamiento entre la rueda y el carril provocando el patinaje de la locomotora.

Existen varias ecuaciones que intentan representar el valor del coeficiente de adherencia rueda – carril, aunque prácticamente todas ellas tienen un denominador común: dependen de la velocidad en cada instante. En nuestro caso, la fórmula empleada para la modelización mediante el programa ha sido:

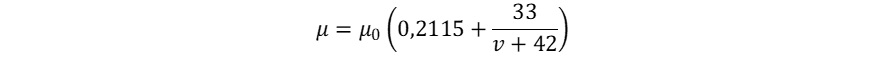
siendo v la velocidad en km/hora y μo el valor del coeficiente de adherencia en el arranque, el cual se ha considerado igual a 0,30.

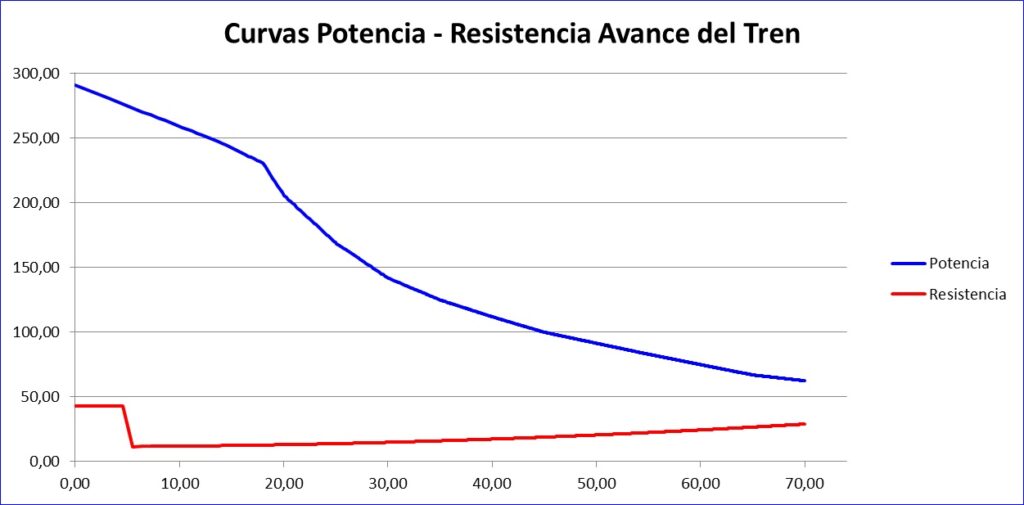
A continuación se muestra a modo de ejemplo la curva de potencia de una locomotora suministrada por su fabricante (curva azul) así como la gráfica de la ecuación de la fuerza de adherencia rueda – carril (curva roja). El eje de accisas representa la velocidad en km/hora. El eje de ordenadas representa la fuerza en kN. El programa analiza en cada momento ambos valores, considerando el menor de los dos como valor de fuerza de tracción en dicho momento.

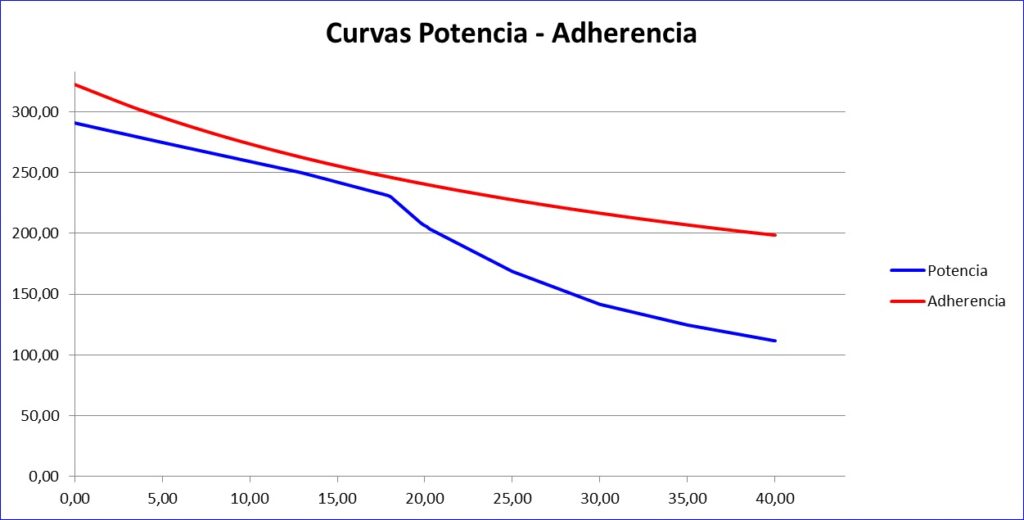
Por tanto, la capacidad de tracción de una locomotora en cada instante será el menor de los valores siguientes:

- - - Fuerza que es capaz de imprimir el motor para la velocidad existente en dicho instante (curva de potencia).
    - Fuerza de adherencia en el contacto rueda – carril para dicha velocidad (curva de adherencia).

Fuerzas resistentes al avance del tren

Las principales fuerzas resistentes al avance del tren son:

Resistencia a la rodadura: debido a que los materiales no tienen una rigidez infinita, el contacto entre la rueda y el carril no se produce en un punto, sino en una pequeña superficie de forma elíptica. Es decir, la rueda “penetra” muy ligeramente en el carril. Esto provoca que la rodadura no sea perfecta, generándose un momento resistente que se opone en todo momento a la rodadura.

Resistencia de los rodamientos: los ejes ferroviarios se conectan al vehículo a través de unos elementos denominados cajas de grasa. Por la misma razón que el fenómeno anterior (la inexistencia de rigidez infinita en los materiales) las zonas de contacto entre ambos elementos no son puntuales, sino pequeñas superficies de contacto, las cuales provocan momentos resistentes durante el giro que resulta necesario vencer.

Resistencias aerodinámicas: son las resistencias más importantes a velocidades elevadas. Dependen de la dirección del aire, de la forma más o menos aerodinámica de los vehículos, de la entrada de aire en el vehículo y de la rugosidad en el contacto aire-superficie del vehículo…

Otras resistencias: existen por último otras resistencias de difícil cuantificación pero que también se oponen al avance del vehículo. Estas son principalmente la resistencia por flexión del carril motivada por el peso de los vehículos, los cuales provocan la deformación de la vía a su paso, y las pérdidas energéticas debidas a los choques de las pestañas de las ruedas contra el carril durante su movimiento.

Los múltiples ensayos para cuantificar la suma de todos estos fenómenos resistivos al avance del tren concluyen que la fórmula matemática que más se aproxima a la realidad es una ecuación parabólica de segundo grado, con la siguiente fórmula:

R = a + bV + cV²

En esta fórmula el valor de “a” cuantifica las resistencias a la rodadura, el valor de “b” cuantifica los rozamientos y choques de las pestañas de las ruedas y el valor de “c” cuantifica las resistencias aerodinámicas.

Resulta importante observar como influye la velocidad en cada término. La resistencia a la rodadura no se ve influenciada por la velocidad, la resistencia causada por los roces y choque de las pestañas de las ruedas es directamente proporcional a la velocidad y las resistencias aerodinámicas son proporcionales a la velocidad al cuadrado. Por ello las resistencias aerodinámicas cobran mucha relevancia en los trenes de alta velocidad.

Los valores de los coeficientes a, b y c de la fórmula varían para los distintos trenes, dependiendo del modelo y longitud de las composiciones. En la bibliografía comentada en la página de inicio pueden encontrarse ejemplos de estos valores.

Fuerza de la gravedad e inscripción de los vehículos en curva

El valor de la fuerza de la gravedad resulta fundamental en las ecuaciones de dinámica ferroviaria dado que, tal y como se explicó en la página de frenado ferroviario, resulta del mismo orden de magnitud que el resto de fuerzas que influyen en el movimiento del tren. Es por ello que el factor más limitante para el transporte de mercancías por ferrocarril es la pendiente de los trazados. Valores de pendientes positivas superiores a las 20 milésimas empiezan a ser limitantes para el transporte de mercancías de forma competitiva respecto a otros medios de transporte debido a la limitación de carga que suponen para los trenes.

Como se explicó en la página de frenado ferroviario, al efecto de la pendiente en alzado hay que añadirle otro impedimento a la rodadura relacionado con el fenómeno de inscripción en curva de los vehículos ferroviarios. Surgen así dos conceptos diferentes de rampa: la rampa real y la rampa ficticia, los cuales fueron explicados en la página de frenado. El valor que ha de ser tenido en cuenta en las ecuaciones de arranque de composiciones ferroviarias es el de la rampa ficticia, por ser más limitante que la rampa real.

Resistencia en el arranque

En el caso de que la velocidad del tren sea igual a cero, es decir, en el momento del arranque de la composición ferroviaria, el valor de la resistencia al avance del tren debería ser el que resulte de la aplicación de las anteriores fórmulas para un valor de V=0. Sin embargo, la experiencia demuestra que estas fórmulas son útiles a partir de cierta velocidad, pero en el momento del arranque de un tren la resistencia al avance es muy superior, siendo normalmente el factor más limitante para establecer la máxima capacidad de carga que puede transportar un tren de mercancías.

Los valores que se suelen tomar para la resistencia en el arranque en rampa varían en función del valor de la rampa, siendo del orden de 70 Newtons por tonelada de peso para rampas menores de 15 milésimas hasta 100 Newtons por tonelada en rampas de 30 milésimas. Se pueden obtenr tablas al respecto en la bibliografía comentada en la introducción.

Masa total del tren y masa rotativa

Como se explica en los libros de física, la velocidad y aceleración que adquiere un sólido bajando por un plano inclinado no solo depende del ángulo del plano inclinado y del coeficiente de rozamiento entre las superficies del plano y del sólido; también depende de si el sólido solo desliza (caso habitual de un sólido de forma rectangular), que deslice y gire, o que solo gire sin deslizar (estos dos últimos casos son los habituales en una rueda o una esfera).

Así por ejemplo, la velocidad final de un sólido rectangular de masa M que deslice sin rozamiento por un plano inclinado es prácticamente un 20% superior a la de un sólido de la misma masa M de forma esférica que, partiendo de la misma altura en reposo, ruede sin deslizar por ese mismo plano. La razón es que mientras en el primer caso toda la energía potencial del sólido se transforma en energía cinética de traslación, en el segundo caso la misma energía potencial se transforma en energía cinética de traslación y de rotación.

Este efecto tiene cierta importancia en el caso de los trenes, dado que los ejes y las ruedas de los vehículos ferroviarios tienen un porcentaje de masa importante en relación a la masa total del vehículo. Debido a ello, en las ecuaciones de tracción y de frenado ferroviarios se tiene en cuenta este hecho a través del denominado “coeficiente de masas giratorias”. Este coeficiente (que habitualmente suele estar entre el 2% y el 8 %) se multiplica por la masa del vehículo para tener en cuenta en las ecuaciones el hecho de que parte de la energía suministrada por los motores sirve para generar energía de rotación en los ejes y ruedas de los vehículos además de energía de traslación. Cabe realizar dos precisiones al respecto:

- - - En el caso de los vehículos de pasajeros y de las locomotoras este coeficiente tiene un valor más constante, pues la masa de los ejes respecto a la masa total de los vehículos no varía en exceso cuando los mismos tienen o no pasajeros. Sin embargo, en los vagones de mercancías este valor puede variar de forma significativa si el vagón está cargado o está vacío. Por esta razón, el programa de tracción ferroviaria aquí presentado permite introducir un porcentaje diferente de masas rotatorias a cada vehículo: locomotoras, vehículo de pasajeros y vehículo de mercancías.
    - Dado que el valor del coeficiente de masas rotatorias es aproximado, podría generar una situación del lado de la inseguridad a la hora de cuantificar la distancia de frenado, al suponer mayor colaboración de la fuerza de la gravedad de la real en las distancias de frenado. Por ello, el programa de cálculo de distancias de frenado tiene en cuenta diferentes valores de coeficiente de masas giratorias si se está en rampa o en pendiente.

Conceptos avanzados

Análisis de las curvas Potencia – Resistencia

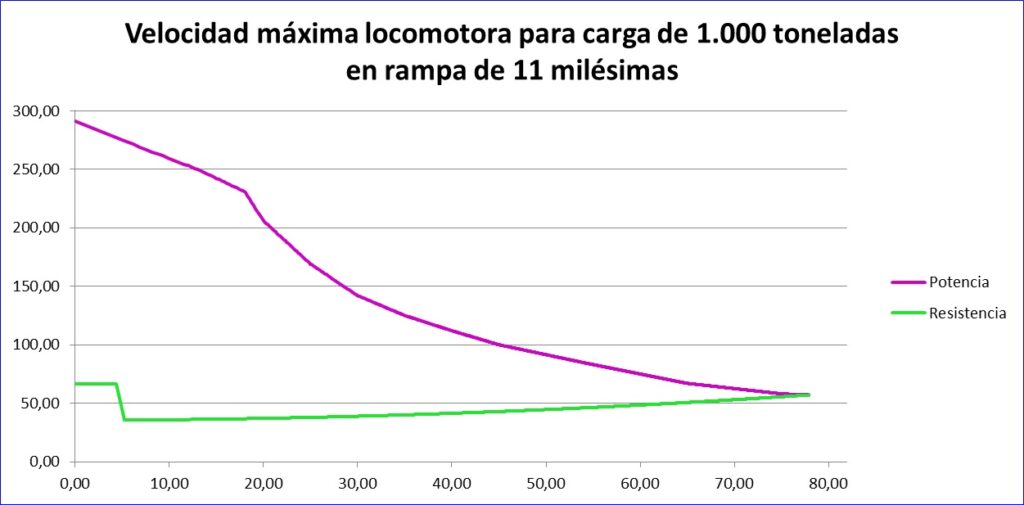
Las curvas de Potencia – Resistencia podrían dividirse en tres zonas, las cuales se han marcado en la imagen inferior. En dicha imagen, pueden verse en azul los valores de la fuerza disponible de las locomotoras del tren o de los ejes tractores del automotor de pasajeros para cada velocidad y en rojo la resistencia que se opone al movimiento del mismo. La gráfica está calculada para un tren de 300 metros de longitud en una recta constante y de pendiente 8 milésimas positivas. Los valores del eje de accisas son la velocidad en km/hora y en ordenadas la fuerza en kN. La línea roja incluye no solo la resistencia por rozamientos y efectos aerodinámicos; incluye también la resistencia al avance por las pendientes del trazado y por la inscripción de la composición ferroviaria en las curvas, que en este ejemplo no existiría por ser el trazado una recta. Como se explicó en la página de frenado ferroviario la longitud del tren, máxime en el momento actual en el que la tendencia europea es fomentar la circulación de trenes de mercancías de gran longitud, influye de forma significativa en el valor de la resistencia al avance por rampa y por inscripción en curva. Los programas presentados en CivilTracks tienen en cuenta este efecto, adaptando el valor de las pendientes y de la inscripción en curvas a la verdadera longitud del tren a través del concepto de «Pendiente ficticia ponderada».

Analicemos las tres zonas señaladas en las curvas:

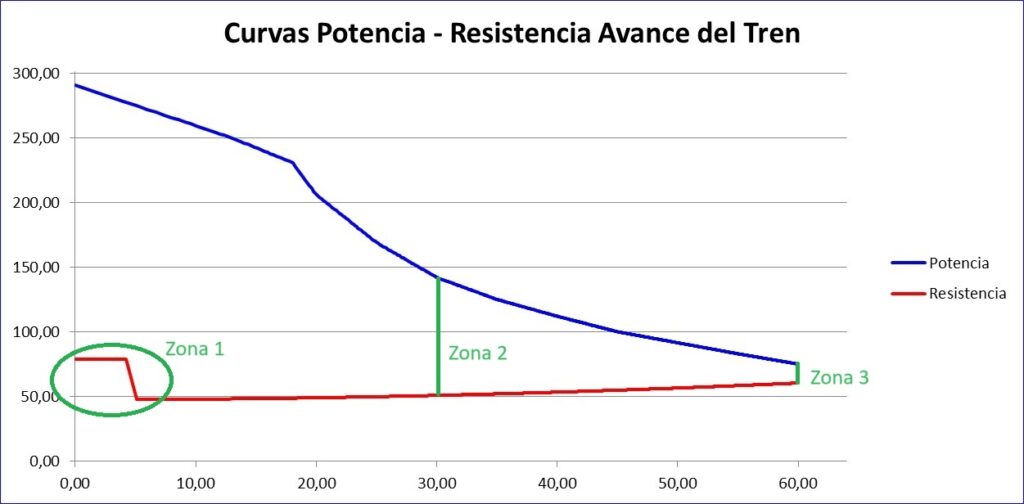
Zona 1: como se ha comentado anteriormente, las ecuaciones parabólicas que simulan los efectos de resistencia al avance de los trenes dan valores muy bajos de resistencia en el momento del arranque del tren. Es por ello que algunas empresas ferroviarias tienen normas que dan valores diferentes de resistencia para el arranque y para velocidades muy bajas. Este efecto provoca un gráfico diferente de resistencia del tren, pues crea un efecto de incremento puntual en la primera zona de la curva de resistencia, la cual es fundamental en el estudio de cargas máximas a transportar por un tren, como se verá posteriormente.

Zona 2: la zona 2 es la zona intermedia de una gráfica Potencia – Resistencia. El valor de la longitud del segmento verde es fundamental en dinámica ferroviaria. Si tenemos en cuenta que la curva azul nos marca la fuerza capaz de ejercer el tren en ese momento y para esa velocidad y en rojo la resistencia al avance en ese mismo momento, la longitud del segmento verde nos dará la fuerza que aun tenemos disponible para acelerar el tren y ganar velocidad.

Zona 3: en esa zona el tren ha llegado a la velocidad máxima a la que se pretendía en el análisis. Vemos que queda un pequeño valor del segmento verde, por lo que aun disponemos de algún esfuerzo tractor. Es lo que se llama aceleración residual, la cual se considera importante principalmente en trenes de viajeros.

Pendientes real, ficticia, ficticia ponderada y pendiente característica

Los conceptos de pendiente real de un trazado, pendiente ficticia y pendiente ficticia ponderada fueron analizados con profundidad en la página de frenado ferroviario, por lo que se comentan aquí de forma somera:

- - - Pendiente real: es la pendiente positiva (rampa) o negativa que va teniendo un trazado ferroviario a lo largo de su recorrido. En el mundo del ferrocarril se suele expresar en milésimas (milímetros por metro de avance).
    - Pendiente ficticia: es el valor de la pendiente real afectado por el rozamiento causado por inscripción de los vehículos en las curvas.
    - Pendiente ficticia ponderada: es una evolución del concepto anterior. Resulta en un concepto matemático que cuantifica el efecto de las pendientes real y ficticia teniendo en cuenta la longitud real del tren, el cual es más importante cuanto mayor es la longitud real del mismo.

Pendiente característica. Una vez conocemos el número y tipo de locomotora disponible para realizar un transporte de mercancías, el dimensionamiento de la máxima carga a transportar se suele hacer buscando la máxima rampa que el tren encontrará a lo largo de todo su recorrido. Esa rampa marcará la máxima carga a transportar. Los administradores de infraestructuras ferroviarias suelen disponer de tablas para cada tipo de locomotora en las que se indica la carga máxima arrancable para dicha locomotora en función de cada valor de pendiente. Una vez se conoce la rampa máxima del recorrido a realizar, acudiendo a dichas tablas se obtendrá la máxima carga transportable.

En una línea ferroviaria, sobre todo en los trazados montañosos más antiguos, puede haber pequeños tramos de corta longitud pero con una pendiente muy pronunciada. Si se dimensionara el tren para el valor de esa pendiente, podría penalizarse en exceso la capacidad de carga de los trenes en esa línea, afectando de forma importante a la explotación comercial de la misma. Por ello surge el concepto de pendiente característica de una línea ferroviaria. Es otro artificio matemático basado en la experiencia y en diferentes estudios, que analiza todas las pendientes a lo largo de una línea ferroviaria y «desprecia» aquellas que por su alto valor pero corta longitud respecto al resto de pendientes de la línea se considera que no deben tenerse en cuenta para dimensionar la carga máxima del tren. De esa manera, si por ejemplo la máxima rampa ficticia de una línea es de 24 milésimas, pero haciendo el estudio de pendientes características se deduce que la máxima rampa característica es de 22 milésimas, se acudirá a las tablas de cargas máximas con el valor de 22 milésimas en vez de 24 milésimas, lo que permitirá el transporte de más carga, por ser una pendiente menor.

El estudio de la verdadera longitud de los trenes en las pendientes reales para ver cómo son afectados por la longitud de las rampas viene a ser un estudio similar al de las pendientes características. Supongamos que disponemos de un tren de 740 metros de longitud, la longitud máxima de tren a la que se están adaptando actualmente muchas estaciones en Europa para fomentar la mejora en el transporte de mercancías. En una línea determinada la mayor rampa es de 26 milésimas en 200 metros de longitud. La rampa anterior del trazado es de 12 milésimas y la posterior es de 16 milésimas. A través del concepto de pendiente ficticia ponderada podremos ver que solo 200 metros de tren están afectados por el valor de 26 milésimas, estando el resto del tren posicionado sobre pendientes menores, por lo que el valor final de la máxima pendiente ficticia ponderada será mucho menor de 26 milésimas; estará en un entorno entre las 16 y las 19 milésimas, permitiéndonos este análisis transportar más carga.

Dimensionamiento de un tren de mercancías

Una vez conocidas las locomotoras disponibles, para el dimensionamiento «teórico más ortodoxo» de la máxima carga a transportar por un tren de mercancías intervendrían principalmente tres premisas, aunque en la práctica resulta muy difícil tenerlas en cuenta todas a la vez, pues penalizaría en exceso la capacidad máxima de transporte de cargas, repercutiendo en la explotación comercial de la línea.

- - - - Primera premisa: garantizar que el tren pueda arrancar desde parado en cualquier punto de la línea. Si por circunstancias de tráfico u otras, el tren tuviera que parar momentáneamente en cualquier punto de la línea con una pendiente muy pronunciada y posteriormente no tuviera potencia suficiente para arrancar desde ese punto, generaría un importante problema en la explotación de dicha línea, al impedir el tráfico del resto de trenes hasta que la situación se restableciera.
      - Segunda premisa: garantizar que el tren circule en todo momento y en cualquier punto de la línea a la máxima velocidad indicada por el cuadro de velocidades de la línea para cada punto kilométrico.
      - Tercera premisa: el tren debe tener una mínima aceleración residual a la máxima velocidad a la que vaya a circular para garantizar la no afectación a la regularidad y explotación de la línea.

El principal criterio por el que se suele fijar la máxima carga transportable por una locomotora es la primera de las premisas anteriormente señaladas: garantizar su arranque en caso de que quedara parado en cualquier punto de la máxima rampa que va a encontrar a lo largo de todo su recorrido. Sin embargo, este criterio no garantiza por sí solo que el tren sea capaz de cumplir la segunda premisa y pueda mantener la máxima velocidad indicada por el cuadro de velocidades de la línea para dicha rampa. En este sentido hay que tener en cuenta que, tal y como ya se ha señalado, cuando un tren que está parado intenta arrancar recibe una mayor resistencia al movimiento que cuando ya tiene cierta velocidad; está en la «Zona 1» de la curva de resistencias. Pero, a cambio, es el momento en el que el motor es capaz de desarrollar la máxima fuerza. Sin embargo, si el mismo tren entra en la rampa a una cierta velocidad (estaría en la «Zona 2» de la curva) puede ocurrir que carezca de suficiente fuerza a esa velocidad para mantener la velocidad deseada. En ese caso, el tren disminuiría sensiblemente su velocidad hasta que termine la rampa o hasta que encuentre una velocidad de equilibrio algo inferior; pero es una situación asumible dada su corta duración durante el trayecto total del tren si tenemos en cuenta que, a cambio, está transportando la mayor carga posible.

Respecto al cumplimiento las premisas primera y segunda de forma conjunta, cabe también destacar un comportamiento aparentemente diferente de las curvas de potencia de las locomotoras eléctricas respecto a las locomotoras diésel. Si se comparan las curvas de varias locomotoras de ambos tipos, se puede observar que en general las locomotoras eléctricas son capaces de mantener la máxima fuerza de la que disponen hasta velocidades del entorno de 60 y 70 km/hora, disminuyendo posteriormente la fuerza disponible. En las líneas antiguas o montañosas, valores del entorno de 60 a 80 km/hora pueden ser perfectamente los valores de máxima velocidad que admita el trazado de esas líneas ferroviarias en los trayectos más accidentados, por lo que estas máquinas serían capaces de suministrar su máxima fuerza con la carga máxima admisible tanto en parada como hasta la máxima velocidad de las rampas más pronunciadas. Sin embargo, las locomotoras diésel generan su máxima fuerza hasta valores de velocidades del entorno de los 20 a 30 km/hora, disminuyendo posteriormente la fuerza disponible, por lo que pueden verse más afectadas a la hora de intentar mantener una velocidad del entorno de 60 a 80 km/hora a carga máxima y en una rampa muy pronunciada.

Al respecto de la tercera premisa, las normas de interoperabilidad europeas para trenes de pasajeros de alta velocidad fijan como criterio que un tren de alta velocidad ha de disponer, una vez llega a su máxima velocidad, de una aceleración residual de al menos 5 cm/s². Esta exigencia, que equivaldría a la tercera premisa previamente expuesta, penalizaría en exceso la capacidad de carga de un tren de mercancías, por lo que no se exige a los trenes de mercancías como uno de los criterios a la hora de dimensionar su máxima carga.

Funcionamiento del programa

El programa general se divide en dos hojas de cálculo, cada una de las cuales es un subprograma en sí mismo:

- - - Datos de trazado y Tren
    - Curvas Potencia – Resistencia

La hoja «Datos de trazado y Tren» permite introducir los datos geométricos de la línea ferroviaria en planta y en alzado, así como los datos del tren. Como se explicará posteriormente, estos datos pueden ser desde una sencilla recta con una pendiente determinada para realizar una comprobación de rampa o carga máxima, hasta todas las alineaciones en planta y alzado de un trazado ferroviario, lo que nos permitirá comprobar en cualquier PPKK del trazado si un tren de una longitud, carga y potencia concretas es capaz de superar una rampa determinada en función de la velocidad inicial que lleve en ese momento, o es capaz de arrancar desde parado en cualquier PPKK que se dese analizar.

La hoja de «Curvas de Potencia – Resistencia» analiza en cada instante de la línea ferroviaria estudiada la máxima fuerza que el tren es capaz de suministrar en función de la velocidad instantánea que tenga en ese momento, así como la resistencia al avance que está sufriendo en función de todos los parámetros que se oponen a dicho avance (rozamientos, efectos aerodinámicos, etc…). A estos valores les añade el efecto de la fuerza de la gravedad debida a las pendientes del trazado en alzado y el efecto de la resistencia por inscripción de los vehículos en curva. La suma global de todos estos efectos determina un valor de fuerza instantánea que, aplicada a la masa global y a la masa rotatoria de la composición ferroviaria, produce una aceleración o deceleración instantáneas. Conociendo la aceleración instantánea, mediante un método multipaso obtenemos la velocidad del tren. Cuando lleguemos a la velocidad objetivo buscada el programa se detendrá y nos mostrará las curvas de potencia y resistencia obtenidas a lo largo de todo el trayecto estudiado.

Algunos aspectos técnicos del programa

Tiempo de cálculo

El tiempo de cálculo del programa es relativamente corto a pesar de la multitud de cálculos internos que realiza. El programa discretiza el trazado en incrementos de tan solo un metro, adaptando la longitud y las masas del tren en todo momento a dicho trazado y analizando las fuerzas aceleradoras y deceleradoras que actúan en cada instante, las cuales son función de la velocidad instantánea del tren, las pendientes en alzado y los radios en planta del trazado en cada metro del mismo. Si se introduce una velocidad final objetivo excesivamente alta para la carga a transportar o la potencia de las locomotoras, el programa seguirá integrando las ecuaciones hasta que deje de haber longitud de trazado suficiente, aspecto que nos indicará mediante un aviso.

Exactitud de los cálculos

Se han realizado comparativas con los datos de cargas y rampas máximas publicados por diferentes fabricantes de locomotoras, obteniéndose valores muy semejantes. No obstante, hay que advertir que el programa se basa en modelos teóricos de comportamiento basados a su vez en fórmulas obtenidas en diferentes estudios realizados a lo largo del tiempo y publicados en la bibliografía y en normativas ferroviarias. Las tablas de cargas y rampas máximas publicadas por los fabricantes se apoyan en pruebas reales de campo por lo que son siempre una referencia muy precisa del funcionamiento y capacidad de carga de dichas locomotoras, al menos para las circunstancias y longitud de trenes para los que se hayan hecho los ensayos de campo.

Datos de trazado y Tren

La hoja de datos de trazado y tren se subdivide en dos zonas claramente diferenciadas: una zona para introducir los datos geométricos del trazado en planta y alzado del trayecto ferroviario modelizado, y otra zona para introducir todos los datos de la composición ferroviaria a analizar: curva de potencia y posición de las locomotoras, longitud, número, masas globales y rotatorias de cada vagón y locomotoras, así como coeficientes aerodinámicos de cada elemento.

La introducción de datos puede parecer algo compleja si no se está familiarizado con el mundo del trazado ferroviario o de carreteras. La razón es que el programa permite modelizar de forma exacta el trazado de toda una línea ferroviaria, con todas sus alineaciones en planta y alzado, así como las características de un tren completo que se desee analizar. No obstante, como se podrá ver posteriormente, la introducción de una simple recta con una pendiente constante y un tren sencillo para comprobar la rampa y carga máxima de dicho tren resulta muy simple.

Datos de trazado en planta y alzado

La introducción de los datos de trazado en planta y alzado para el programa de «Tracción Ferroviaria» es similar a la del programa de «Frenado de Tren». Es por ello que se recomienda al lector la lectura del capítulo Datos de Trazado de dicho programa, donde se dan todas las indicaciones necesarias para introducir un trazado sencillo (una simple recta con una pendiente determinada) o el trazado completo y exacto de una línea ferroviaria, con todas sus rectas, curvas, cambios bruscos de curvatura, clotoides completas, incompletas y de vértice en planta, así como sus pendientes y acuerdos parabólicos en alzado.

Datos específicos del tren

En la zona de datos del tren introduciremos todas las características de la composición ferroviaria a analizar.

- - Longitud de los vagones y locomotoras: el programa supone la misma longitud para todos los elementos. Si hubiera varias longitudes de vehículo, se puede tomar un valor que sea múltiplo de todos los valores y simular el resto de vehículos como múltiplos de la misma.
  - Distancia enganche: nos permite analizar la fuerza instantánea en el enganche de cualquiera de los vehículos a lo largo de todo el trayecto.
  - Curva de potencia: en esta zona introduciremos todos los valores de la curva de potencia de las locomotoras que realizarán la tracción del tren. Se pueden introducir hasta 40 pares de valores Velocidad (en Km/h) – Fuerza (en kN) para modelizar la curva.
  - Peso Tren: en esta zona introduciremos los pesos por metro lineal de los vehículos (en Toneladas/metro) así como el coeficiente de masas giratorias de cada uno. En otra columna introduciremos una S si el vehículo es tractor (una locomotora en el caso de de trenes de mercancías o un vehículo con ejes tractores en el caso de un automotor de viajeros). Cada vez que introduzcamos una S el programa considerará la curva de potencia aplicada a dicho vehículo. Por tanto si hay tres S en la composición el programa considerará que hay tres locomotoras, lo cual permite simular trenes con doble tracción en cabeza o trenes con tracción en cabeza y tracción en zonas intermedias.
  - Coeficientes de pérdidas: en esta zona introduciremos los coeficientes a,b,c de pérdidas por rozamientos y aerodinámicas de cada vehículo. Estos valores se introducen en decaNewtons por tonelada, por lo que si un vehículo mide por ejemplo 20 metros y pesa 4 Tn/m, el programa considerará el valor de 80 toneladas aplicado a los coeficientes a, b, c.

A continuación veremos varios ejemplos de entrada de datos:

Ejemplo 1

El primer ejemplo consiste en analizar la capacidad de un tren para arrancar en una rampa de 6 milésimas, así como ver cual es la máxima velocidad que es capaz de alcanzar en dicha rampa. Los datos de entrada del trazado son:

- - - PPKK inicial: 0
    - Ancho de vía internacional: 1.435 mm
    - Longitud de la recta: suponemos 25.000 metros para que haya suficiente longitud en el análisis numérico
    - Pendiente de la recta: 6 milésimas
    - Acuerdo vertical: suponemos un acuerdo vertical en el PPKK 30.000. Como se explica en la página de frenado ferroviario, el programa necesita tener como mínimo un acuerdo. Al simular ese acuerdo en el PPKK 30.000 y terminar el trazado en el PPKK 25.000 a efectos prácticos dicho acuerdo no influye en los cálculos, por lo que toda la recta se mantendrá con pendiente constante de 6 milésimas.

Los datos de entrada de tren son:

- - - Curva de potencia: se ha introducido la curva de potencia de una locomotora real.
    - Distancia enganche: se pretende analizar la fuerza que soporta el enganche entre el sexto y séptimo vagón (120 metros).
    - Longitud del tren: el tren mide en total 440 metros, dado que son 22 vehículos de 20 metros de longitud.
    - Peso de los vehículos: la locomotora pesa 110 toneladas (20 metros x 5,5 Tn/m). Respecto a los vagones, se han supuesto casi todos los vagones cargados a carga máxima, excepto los vagones 10 a 14 y 19 a 22 que se han supuesto sin carga, solo con el peso en vacío del vagón. Por esa razón los coeficientes de masas giratorias son diferentes. Los coeficientes de pérdidas se han supuesto diferentes en la locomotora de cabeza que en los vagones.

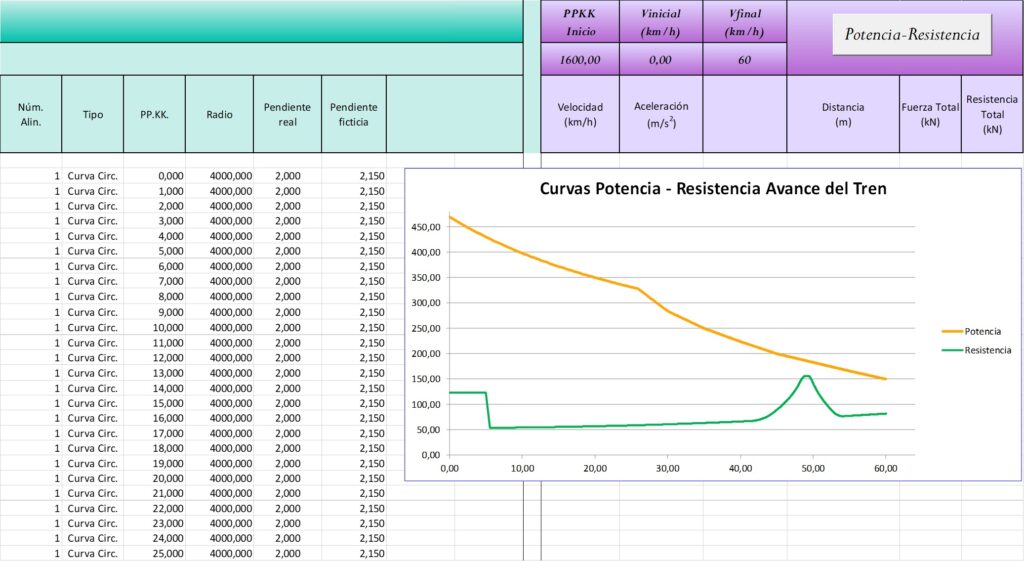
A continuación se muestra la pantalla de datos de entrada:

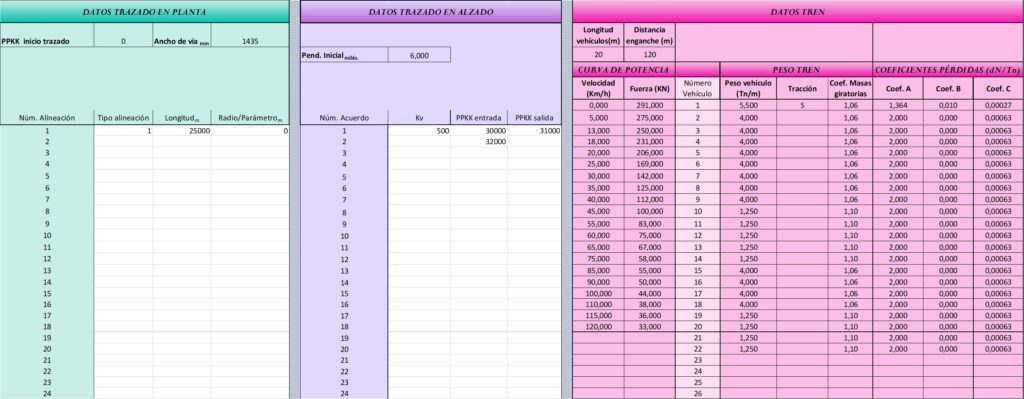
Ejemplo 2

En el ejemplo 2 vamos a comprobar la capacidad de un tren europeo interoperable (740 metros de longitud) con doble tracción por cabeza de tren para arrancar en una curva de radio 4.000 metros y rampa de 4 milésimas y, una vez adquirida cierta velocidad, analizar su comportamiento ante una rampa de 14 milésimas. Los datos de entrada del trazado son:

- - - PPKK inicial: 0
    - Ancho de vía internacional: 1.435 mm
    - Longitud de la curva: suponemos 10.000 metros para que haya suficiente longitud en el análisis numérico
    - Pendientes en alzado de la curva: la pendiente inicial son 4 milésimas. En el PPKK 2.000 aparece un acuerdo parabólico cóncavo de 100 metros de longitud que modifica la pendiente del trazado a 14 milésimas. El trazado en alzado continúa durante 200 metros con una pendiente de 14 milésimas (de los PPKK 2.100 a 2.300) para, posteriormente, volver a bajar a 4 milésimas a través de otro acuerdo de la misma longitud pero de signo contrario (acuerdo parabólico convexo). A partir del PPKK 2.400 la pendiente continúa a 4 milésimas hasta el PPKK 30.000 (se ha introducido un valor alto, el cual siempre ha de ser igual o superior al mayor PPKK de trazado en planta, para que haya suficientes datos).

Los datos de entrada de tren son:

- - - Curva de potencia: se ha introducido la misma curva de potencia de la locomotora del ejemplo anterior, pero en este caso al aparecer una «S» en los dos primeros vehículos, significa que ambos vehículos son tractores (son dos locomotoras), por lo que el programa aplica la curva de potencia a cada uno de los dos vehículos, duplicando la capacidad de tracción del tren.
    - Distancia enganche: se pretende analizar la fuerza que soporta el enganche en la conexión del primer vagón con las locomotoras (40 metros).
    - Longitud del tren: el tren mide en total 740 metros, dado que son 37 vehículos de 20 metros de longitud.
    - Peso de los vehículos: las locomotoras pesan 110 toneladas (20 metros x 5,5 Tn/m). Respecto a los vagones, se han supuesto todos los vagones cargados a su carga máxima. Los coeficientes de pérdidas se han supuesto diferentes en la locomotora de cabeza que en el resto de vehículos.

A continuación se muestra la pantalla de datos de entrada:

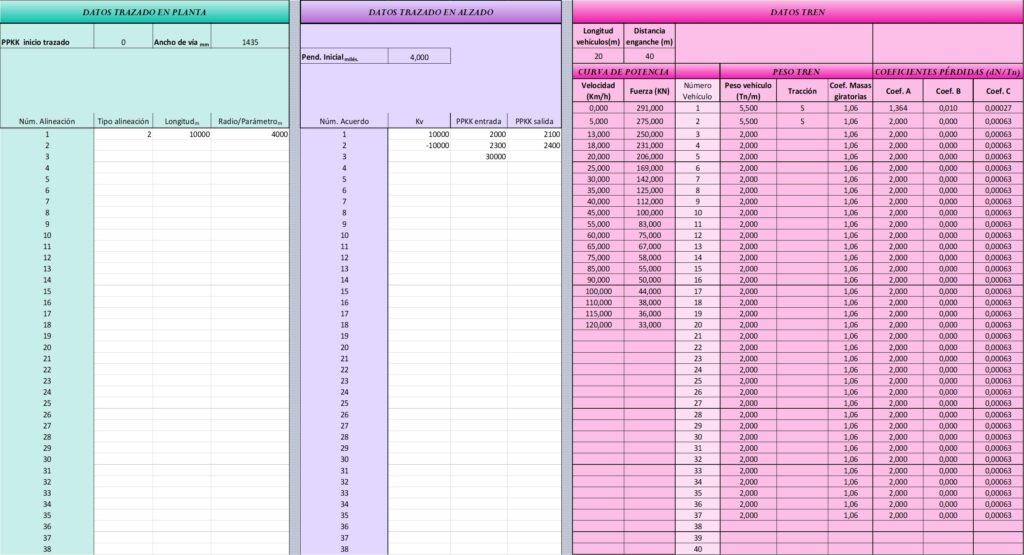
Resultados

En la hoja de resultados resulta necesario introducir unos últimos datos de entrada. Estos son:

- - - PPKK de inicio del cálculo
    - Velocidad inicial del tren
    - Velocidad final objetivo

El programa permite iniciar el cálculo en cualquier PPKK del trazado definido previamente en la hoja de datos de entrada. No obstante han de cumplirse dos premisas:

- - - - El PPKK inicial de cálculo ha de ser superior al PPKK inicial del trazado más la longitud total del tren, lo cual garantiza que todo el tren está dentro del trazado.
      - La longitud total de trazado ha de ser suficiente para desarrollar todo el cálculo hasta la velocidad final objetivo o hasta la velocidad de equilibrio.

Respecto a la velocidad inicial, el programa permite considerar una velocidad inicial de 0 km/hora, lo cual nos garantiza poder estudiar la capacidad de arranque del tren en cualquier PPKK del trazado, aspecto crucial en el dimensionamiento de la máxima carga transportable por un tren. Por otra parte, podemos introducir una velocidad inicial distinta de cero para estudiar el comportamiento de un tren cuando entra en un trazado especialmente sinuoso en planta y/o alzado con una velocidad inicial previamente establecida.

Por último, la velocidad final objetivo en un valor que puede o no alcanzarse. Si introducimos un valor alcanzable, el programa realizará los cálculos hasta llegar a la velocidad fijada, pudiendo obtenerse la distancia que ha necesitado el tren para llegar a dicha velocidad y la aceleración y velocidad instantáneas que ha tenido en cada momento del recorrido. Si la velocidad final objetivo es muy alta, el programa se detendrá cuando llegue al final del trazado y nos avisará del suceso. Este hecho puede ocurrir por dos motivos:

- - - Falta de longitud de trazado suficiente, lo cual se soluciona introduciendo más longitud de trazado en la hoja de datos de entrada.
    - Falta de potencia suficiente para la velocidad objetivo deseada. En este caso, se producirá un momento en el cálculo en el que se llegue a una «velocidad de equilibrio». Según se ha explicado previamente, a medida que el tren gana velocidad, disminuye su capacidad de tracción (según se puede observar en las curvas de potencia de un tren) a la vez que aumenta la resistencia al avance (se puede observar en la curva de resistencias cuando el valor de la pendiente es constante). En el momento que ambas fuerzas se equilibran el tren no puede incrementar su velocidad, por lo que la velocidad se mantendrá constante bien hasta que el trazado finalice, bien hasta que se produzca un cambio de trazado, como pudiera ser una disminución de la pendiente. Por tanto, simulando un trazado en recta y pendiente constante e introduciendo una velocidad objetivo suficientemente alta en el programa, podemos hallar la velocidad máxima de una locomotora para una carga y rampa prefijadas.

A continuación se analizan los resultados obtenidos tras el cálculo de los ejemplos 1 y 2.

Ejemplo 1

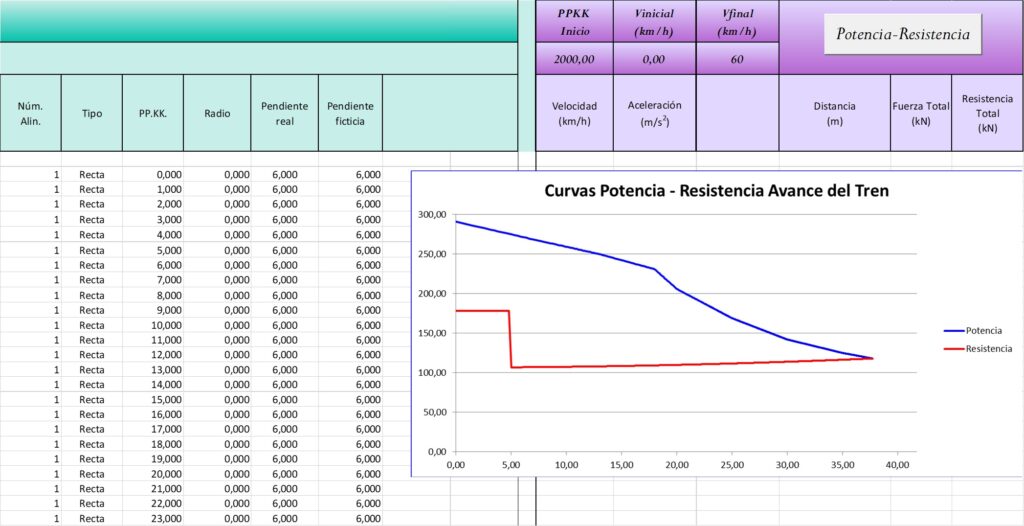
Como se puede ver en los listados, el tren arranca desde parado en el PPKK 2.000 e intenta llegar a la velocidad de 60 km/hora. Las rampas real y ficticia son del mismo valor, dado que estamos en una recta. Vemos como el tren no tiene problema en el arranque, dado que existe una gran distancia entre el valor de máxima fuerza disponible (270 Kn) y la máxima resistencia en arranque (170 kN). Tras superar la zona de arranque, la curva roja de resistencia al movimiento (se recuerda que el programa incluye en dicha curva de forma conjunta los valores de resistencia por rozamientos y por pendiente del trazado) disminuye bruscamente para ir subiendo progresivamente pero de una manera muy suave, pues estamos en una zona de bajas velocidades, por lo que el término de cV² apenas influye. Sin embargo, la fuerza de la locomotora baja significativamente a partir de los 20 km/hora. En el momento que ambas curvas se cruzan se produce la «velocidad de equilibrio». La fuerza que genera el tren a esa velocidad es la misma que la suma de fuerzas resistentes que se oponen a su avance, por lo que la aceleración resultante es 0 m/s². El programa sigue calculando hasta el final del trazado pues no hay nada que lo impida, pero la velocidad en los listados de resultados se mantiene constante. En definitiva, la locomotora modelizada es capaz de arrancar la carga dispuesta hasta el entorno de 38 km/hora pero no puede llegar hasta 60 km/hora salvo que a partir de cierto punto del trazado disminuyera la pendiente de seis milésimas.

Ejemplo 2

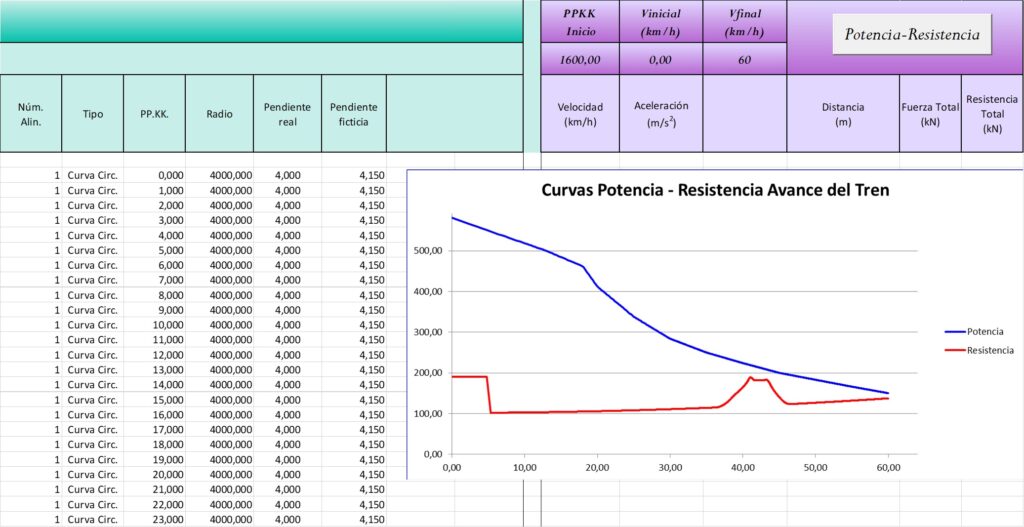
El ejemplo 2 muestra todo el potencial de cálculo y análisis del programa gracias a la realización interna de cálculos mediante métodos multipaso. El tren va en doble tracción y mide 740 metros. Dado que el trazado en planta está en curva, podemos ver como la pendiente ficticia es algo superior a la pendiente real (4,15 milésimas frente a 4 milésimas). El tren comienza su marcha en el PPKK 1.600 con una pendiente muy suave de 4 milésimas e intenta llegar a la velocidad 60 km/hora. Pero en su camino se interpone una rampa de cierto valor como son 14 milésimas, aunque de corta longitud en relación a la longitud total del tren. Vemos como la curva de resistencias (que incluye el valor de resistencia por rampa, la cual va variando metro a metro durante el paso por los acuerdos parabólicos verticales) comienza a subir de forma significativa a partir del comienzo del acuerdo cóncavo. Llega a un pico irregular causado por el hecho de que los 40 primeros metros del tren tienen una carga por metro diferente al resto del tren (5,5 Tn/metro frente a 2 Tn/metro). La resistencia al avance se mantiene estable pero alta durante un tramo para luego bajar progresivamente según el tren va pasando por el acuerdo convexo y empezando a volver a la pendiente de 4 milésimas. El hecho de que en todo momento exista una cierta distancia entre la curva azul de fuerza de tracción y la roja de resistencias garantiza que el tren tiene fuerza suficiente para mantener e incluso aumentar sensiblemente la velocidad en la zona de rampa pronunciada. Posteriormente, el tren sigue aumentando su velocidad hasta llegar a los 60 km/hora, quedándole incluso una cierta capacidad de aceleración residual (Zona 3 de las curvas). Dado que era la velocidad final objetivo, el programa detiene los cálculos, mostrando las gráficas de resultados y los listados de velocidad y aceleración instantáneas, así como la distancia total que el tren ha necesitado para llegar a la velocidad objetivo.